ADMINISTRAÇÃO: Integrais

quinta-feira, 2 de abril de 2009

Integrais

Propriedades da Integral Indefinida

$\int cf(x)\,dx = c\int f(x)\,dx$

$\int [f(x) + g(x)]\,dx = \int f(x)\,dx + \int g(x)\,dx$

$\int f(x)g(x)\,dx = f(x)\int g(x)\,dx - \int \left(d[f(x)]\int g(x)\,dx\right)dx$ ou, de outra forma,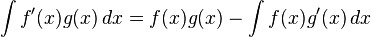

$\int f'(x)g(x)\,dx = f(x)g(x) - \int f(x)g'(x)\,dx$

Integrais Indefinidas de Funções Simples

Funções Racionais

$\int x^n\,dx = \frac{x^{n+1}}{n+1} + C\qquad\mbox{ para }n \ne -1$

$\int \frac{1}{x}\,dx = \ln{\left|x\right|} + C$

$\int \frac{1}{a^2+x^2} \, dx = \frac{1} {a} arctan({x}/{a}) + C$

Logaritmos

$\int \log_b {x}\,dx = x\log_b {x} - x\log_b {e} + C$

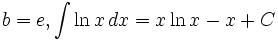
Caso particular: $b = e, \int \ln {x}\,dx = x \ln {x} - x + C$

Funções Exponenciais

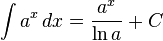
$\int a^x\,dx = \frac{a^x}{\ln{a}} + C$

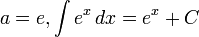
Caso particular: $a = e, \int e^x\,dx = e^x + C$

Funções Irracionais

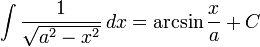
$\int {1 \over \sqrt{a^2-x^2}} \, dx = \arcsin {\frac{x}{a}} + C$

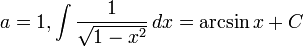
Caso particular: $a = 1, \int {1 \over \sqrt{1-x^2}}\, dx = \arcsin {x} + C$

$\int {-1 \over \sqrt{a^2-x^2}} \, dx = \arccos {\frac{x}{a}} + C = (-1)arcsin {\frac{x}{a}} + C$

Caso particular: $a = 1, \int {-1 \over \sqrt{1-x^2}} \, dx = \arccos {x} + C$

Funções Trigonométricas

$\int \cos{x} \, dx = \sin{x} + C$

$\int \sin{x} \, dx = -\cos{x} + C$

$\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C$

$\int \csc{x} \, dx = \ln{\left| \csc{x} - \cot{x}\right|} + C$

$\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C$

$\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C$

$\int \sec{x} \tan{x} \, dx = \sec {x} + C$

$\int \csc{x} \cot{x} \, dx = -\csc {x} + C$

$\int \sec^2 x \, dx = \tan x + C$

$\int \csc^2 x \, dx = -\cot x + C$

$\int \sin^2 x \, dx = \frac{1}{2}(x - \sin x \cos x) + C$

$\int \cos^2 x \, dx = \frac{1}{2}(x + \sin x \cos x) + C$

Funções Hiperbólicas

$\int \sinh x \, dx = -\cosh x + C$

$\int \cosh x \, dx = \sinh x + C$

$\int \tanh x \, dx = \ln (\cosh x) + C$

$\int \mbox{csch}\,x \, dx = \ln\left| \tanh {x \over2}\right| + C$

$\int \mbox{sech}\,x \, dx = \arctan(\sinh x) + C$

$\int \coth x \, dx = \ln|\sinh x| + C$

Integrais Impróprias

Existem funções cujas antiderivadas não podem ser expressas de forma fechada. No entanto, os valores das integrais definidas dessas funções em intervalos comuns podem ser calculados. Algumas integrais definidas de uso frequente estão relacionadas abaixo.

$\int_0^\infty{\sqrt{x}\,e^{-x}\,dx} = \frac{1}{2}\sqrt \pi$

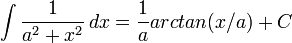
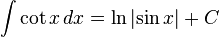
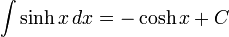
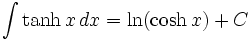
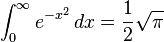
$\int_0^\infty{e^{-x^2}\,dx} = \frac{1}{2}\sqrt \pi$

$\int_0^\infty{\frac{x}{e^x-1}\,dx} = \frac{\pi^2}{6}$

$\int_0^\infty{\frac{x^3}{e^x-1}\,dx} = \frac{\pi^4}{15}$

$\int_0^\infty\frac{\sin(x)}{x}\,dx=\frac{\pi}{2}$

fonte: http://pt.wikipedia.org/wiki/T%C3%A1bua_de_integrais

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)