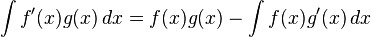ADMINISTRAÇÃO: 04/01/2009

sexta-feira, 17 de abril de 2009

As Cinco Forças de Porter

“Posicione a sua indústria onde as forças são mais fracas” (Michael Porter)

Porter apresenta uma metodologia analítica para que se compreendam as indústrias e a concorrência para a formulação de uma estratégia competitiva global (não só responde ao meio ambiente, mas também tenta modelar este meio ambiente em favor de uma empresa). Ele descreve as cinco forças competitivas como determinam a rentabilidade e a atratividade de uma indústria.

As cinco forças são: A entrada de novos concorrentes, a ameaça de substitutos, o poder de negociação dos compradores, o poder de negociação dos fornecedores e a rivalidade entre os concorrentes existentes.

Novos entrantes -> Empresas que entram no mercado querendo uma fatia de determinado setor. Caso haja barreiras de entradas que possam dificultar a sua inserção, fica mais difícil a sua fixação no mercado. Exemplo de barreiras: Diferenciação do produto, identidade da marca.

Fornecedores-> O poder de negociação dos fornecedores determina os custos dos insumos de matéria-prima. Eles são uma fonte de poder. Fornecedores podem recusar-se a trabalhar com a empresa, ou, por exemplo, cobrar preços excessivamente elevados para recursos únicos.

Substitutos -> A existência de produtos (bens e serviços) substitutos no mercado, que analisados, desempenham funções equivalentes ou parecidas é uma condição básica de barganha que pode afetar as empresas

Compradores-> Os clientes exigem mais qualidade por um menor preço de bens e serviços. Também competindo com a indústria, forçando os preços para baixo. Assim jogando os concorrentes uns contra os outros.

Rivalidade entre concorrentes -> Para a maioria das indústrias, esse é o principal determinante da competitividade do mercado. Às vezes rivais competem agressivamente, não só em relação ao preço do produto, como também a inovação, marketing, etc.

As cinco forças competitivas segundo Porter irão determinar a rentabilidade da indústria porque irão influenciar os preços, os custos e o investimento necessário das empresas em uma indústria.
O vigor das cinco forças varia de indústria para indústria podendo modificar-se ao longo tempo. O resultado é que todas as indústrias não são semelhantes, sendo assim, em indústrias onde as cinco forças são favoráveis, muitos concorrentes obtém retornos. Mas em empresas onde a pressão de uma ou mais das cinco forças é intensa (linhas aéreas, têxteis), poucas empresas comandam retornos atrativos.

Em qualquer indústria particular nem todas essas cindo forças terão igual importância.
A metodologia das cinco forças permite quem uma empresa perceba a complexidade e aponte os fatores críticos para concorrência em sua indústria bem como permite que ela identifique as inovações estratégicas que melhorariam a rentabilidade da indústria e a sua própria.

Bibliografia: Vantagm competitiva (Michael Porter)

quinta-feira, 2 de abril de 2009

Integrais

Propriedades da Integral Indefinida

$\int cf(x)\,dx = c\int f(x)\,dx$

$\int [f(x) + g(x)]\,dx = \int f(x)\,dx + \int g(x)\,dx$

$\int f(x)g(x)\,dx = f(x)\int g(x)\,dx - \int \left(d[f(x)]\int g(x)\,dx\right)dx$ ou, de outra forma,

$\int f'(x)g(x)\,dx = f(x)g(x) - \int f(x)g'(x)\,dx$

Integrais Indefinidas de Funções Simples

Funções Racionais

$\int x^n\,dx = \frac{x^{n+1}}{n+1} + C\qquad\mbox{ para }n \ne -1$

$\int \frac{1}{x}\,dx = \ln{\left|x\right|} + C$

$\int \frac{1}{a^2+x^2} \, dx = \frac{1} {a} arctan({x}/{a}) + C$

Logaritmos

$\int \log_b {x}\,dx = x\log_b {x} - x\log_b {e} + C$

Caso particular: $b = e, \int \ln {x}\,dx = x \ln {x} - x + C$

Funções Exponenciais

$\int a^x\,dx = \frac{a^x}{\ln{a}} + C$

Caso particular: $a = e, \int e^x\,dx = e^x + C$

Funções Irracionais

$\int {1 \over \sqrt{a^2-x^2}} \, dx = \arcsin {\frac{x}{a}} + C$

Caso particular: $a = 1, \int {1 \over \sqrt{1-x^2}}\, dx = \arcsin {x} + C$

$\int {-1 \over \sqrt{a^2-x^2}} \, dx = \arccos {\frac{x}{a}} + C = (-1)arcsin {\frac{x}{a}} + C$

Caso particular: $a = 1, \int {-1 \over \sqrt{1-x^2}} \, dx = \arccos {x} + C$

Funções Trigonométricas

$\int \cos{x} \, dx = \sin{x} + C$

$\int \sin{x} \, dx = -\cos{x} + C$

$\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C$

$\int \csc{x} \, dx = \ln{\left| \csc{x} - \cot{x}\right|} + C$

$\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C$

$\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C$

$\int \sec{x} \tan{x} \, dx = \sec {x} + C$

$\int \csc{x} \cot{x} \, dx = -\csc {x} + C$

$\int \sec^2 x \, dx = \tan x + C$

$\int \csc^2 x \, dx = -\cot x + C$

$\int \sin^2 x \, dx = \frac{1}{2}(x - \sin x \cos x) + C$

$\int \cos^2 x \, dx = \frac{1}{2}(x + \sin x \cos x) + C$

Funções Hiperbólicas

$\int \sinh x \, dx = -\cosh x + C$

$\int \cosh x \, dx = \sinh x + C$

$\int \tanh x \, dx = \ln (\cosh x) + C$

$\int \mbox{csch}\,x \, dx = \ln\left| \tanh {x \over2}\right| + C$

$\int \mbox{sech}\,x \, dx = \arctan(\sinh x) + C$

$\int \coth x \, dx = \ln|\sinh x| + C$

Integrais Impróprias

Existem funções cujas antiderivadas não podem ser expressas de forma fechada. No entanto, os valores das integrais definidas dessas funções em intervalos comuns podem ser calculados. Algumas integrais definidas de uso frequente estão relacionadas abaixo.

$\int_0^\infty{\sqrt{x}\,e^{-x}\,dx} = \frac{1}{2}\sqrt \pi$